LeNet-5 CNN
Implementation of LeNet-5 CNN with PyTorch

In this notebook, we will implement the LeNet-5 convolutional neural network architecture with the help of PyTorch. This notebook has been adapted from one of the tutorials presented during a workshop at the Applied Machine Learning Days 2020.
The LeNet-5 architecture
The LeNet-5 CNN architecture was introduced by Yann LeCun, Leon Bottou, Yosuha Bengio and Patrick Haffner back in 1990's to recognise the handwritten and machine printed characters. Since then, due to its simplicity, it has been used as a first step in teaching Convolutional Neural Networks.
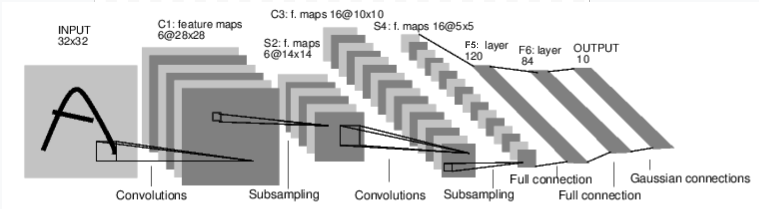
Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. "Gradient-based learning applied to document recognition." Proceedings of the IEEE, 86(11):2278-2324, November 1998.
Details of the architecture
Note : In the following, convolutional layers are labeled as Cx, subsampling layers are labeled as Sx, and fully connected layers are labeled as Fx, where x is the layer index.
- Convolutional part:
| Layer | Name | Input channels | Output channels (number of kernels) | Kernel size | stride |
|---|---|---|---|---|---|
| Convolution | C1 | 1 | 6 | 5x5 | 1 |
| tanh | 6 | 6 | |||
| AvgPooling | S2 | 6 | 6 | 2x2 | 2 |
| Convolution | C3 | 6 | 16 | 5x5 | 1 |
| tanh | 16 | 16 | |||
| AvgPooling | S4 | 16 | 16 | 2x2 | 2 |
| Convolution | C5 | 6 | 120 | 5x5 | 1 |
| tanh | 120 | 120 |
- Fully Connected part:
| Layer | Name | Input size | Output size |
|---|---|---|---|
| Linear | F5 | 120 | 84 |
| tanh | |||
| Linear | F6 | 84 | 10 |
| LogSoftmax |
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.set_printoptions(precision=3)
import sys
! pip -q install colorama
import colorama # for producing colored terminal text and cursor positioning
from collections import OrderedDict
import matplotlib.pyplot as plt
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self.conv_net = nn.Sequential(OrderedDict([ # We use Ordered dictionary object here. They remember the order that items were inserted. When iterating over an ordered dictionary, the items are returned in the order their keys were first added.
('C1', nn.Conv2d(1, 6, kernel_size=(5, 5))),
('Tanh1', nn.Tanh()),
('S2', nn.AvgPool2d(kernel_size=(2, 2), stride=2)),
('C3', nn.Conv2d(6, 16, kernel_size=(5, 5))),
('Tanh3', nn.Tanh()),
('S4', nn.AvgPool2d(kernel_size=(2, 2), stride=2)),
('C5', nn.Conv2d(16, 120, kernel_size=(5, 5))),
('Tanh5', nn.Tanh()),
]))
self.fully_connected = nn.Sequential(OrderedDict([
('F6', nn.Linear(120, 84)),
('Tanh6', nn.Tanh()),
('F7', nn.Linear(84, 10)),
('LogSoftmax', nn.LogSoftmax(dim=-1))
]))
def forward(self, imgs):
output = self.conv_net(imgs)
output = output.view(imgs.shape[0], -1) # imgs.shape[0] is the batch_size
output = self.fully_connected(output)
return output
Now that we have created our model, let's print the summary to check if everything is correct.
conv_net = LeNet5()
print(conv_net)
Our architecture looks perfect !
def train_cnn(model, train_loader, test_loader, device, num_epochs=3, lr=0.1):
""" Trains the LeNet-5 CNN """
# We define an optimizer and a loss function
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
criterion = torch.nn.CrossEntropyLoss()
for epoch in range(num_epochs):
print("=" * 30, "Starting epoch %d" % (epoch + 1), "=" * 30)
model.train() # Not necessary in our example, but still good practice.
# Only models with nn.Dropout and nn.BatchNorm modules require it
# dataloader returns batches of images for 'data' and a tensor with their respective labels in 'labels'
for batch_idx, (data, labels) in enumerate(train_loader):
data, labels = data.to(device), labels.to(device)
optimizer.zero_grad()
output = model(data)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
if batch_idx % 40 == 0:
print("Batch %d/%d, Loss=%.4f" % (batch_idx, len(train_loader), loss.item()))
# Compute the train and test accuracy at the end of each epoch
train_acc = accuracy(model, train_loader, device)
test_acc = accuracy(model, test_loader, device)
print(colorama.Fore.GREEN, "\nAccuracy on training: %.2f%%" % (100*train_acc))
print("Accuracy on test: %.2f%%" % (100*test_acc), colorama.Fore.RESET)
def accuracy(model, dataloader, device):
""" Computes the model's accuracy on the data provided by 'dataloader'
"""
model.eval()
num_correct = 0
num_samples = 0
with torch.no_grad(): # deactivates autograd, reduces memory usage and speeds up computations
for data, labels in dataloader:
data, labels = data.to(device), labels.to(device)
predictions = model(data).max(1)[1] # indices of the maxima along the second dimension
num_correct += (predictions == labels).sum().item()
num_samples += predictions.shape[0]
return num_correct / num_samples
from torchvision import datasets, transforms
transformations = transforms.Compose([
transforms.Resize((32, 32)),
transforms.ToTensor()
])
train_data = datasets.MNIST('./data',
train = True,
download = True,
transform = transformations)
test_data = datasets.MNIST('./data',
train = False,
download = True,
transform = transformations)
train_loader = torch.utils.data.DataLoader(train_data, batch_size=256, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=1024, shuffle=False)
plt.figure(figsize=(16,9))
data, target = next(iter(train_loader))
for i in range(10):
img = data.squeeze(1)[i]
plt.subplot(1, 10, i+1)
plt.imshow(img, cmap="gray", interpolation="none")
plt.xlabel(target[i].item(), fontsize=18)
plt.xticks([])
plt.yticks([])
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # Check if gpu available
conv_net = conv_net.to(device)
train_cnn(conv_net, train_loader, test_loader, device, num_epochs=10, lr=2e-3)
Accuracy of 98.58% on the test set, excellent ! If one notice carefully, our model already achieved an accuracy of 98.70% after the end of 8th epoch. In further two epochs, we are overfitting our model and that's why the accuracy on the test set drops. This can be avoided by keeping track of the loss values.
def visualize_predictions(model, dataloader, device):
data, labels = next(iter(dataloader))
data, labels = data[:10].to(device), labels[:10]
predictions = model(data).max(1)[1]
predictions, data = predictions.cpu(), data.cpu()
plt.figure(figsize=(16,9))
for i in range(10):
img = data.squeeze(1)[i]
plt.subplot(1, 10, i+1)
plt.imshow(img, cmap="gray", interpolation="none")
plt.xlabel(predictions[i].item(), fontsize=18)
plt.xticks([])
plt.yticks([])
visualize_predictions(conv_net, test_loader, device)
Let me know if you have any feedback or comments !